1. 嵌段共聚物非平衡態(tài)自組裝行為及其機(jī)理
嵌段共聚物體系在納米尺度上形成的有序結(jié)構(gòu)是獲取新型高分子材料所需要的聚集態(tài)結(jié)構(gòu)的重要來源之一�。但是�,由于線形AB兩嵌段共聚物體系能夠形成的穩(wěn)定納米有序結(jié)構(gòu)數(shù)目十分有限,而采用多組分嵌段共聚物體系和更為復(fù)雜的高分子鏈拓?fù)浣Y(jié)構(gòu)來獲取所需要的穩(wěn)定納米有序結(jié)構(gòu)又需要十分復(fù)雜的化學(xué)合成過程���,不利于成本的降低����,因此�����,如何調(diào)控簡(jiǎn)單嵌段共聚物體系的非平衡態(tài)結(jié)構(gòu)演化動(dòng)力學(xué)過程來獲取所需要的納米有序結(jié)構(gòu)(非平衡態(tài)過程控制自組裝)就變得十分具有吸引力。其中的關(guān)鍵在于如何構(gòu)建簡(jiǎn)單嵌段共聚物體系中的不穩(wěn)定狀態(tài)�����,從而使由構(gòu)建的不穩(wěn)定狀態(tài)出發(fā)的非平衡態(tài)結(jié)構(gòu)演化動(dòng)力學(xué)過程最終到達(dá)人們所需要的納米有序結(jié)構(gòu)�����。盡管由非平衡態(tài)結(jié)構(gòu)演化動(dòng)力學(xué)過程俘獲的納米有序結(jié)構(gòu)一般是亞穩(wěn)定的�,但是��,由于嵌段共聚物體系具有極其崎嶇不平的自由能曲面���,穩(wěn)定的納米有序結(jié)構(gòu)和亞穩(wěn)定的納米有序結(jié)構(gòu)之間的勢(shì)壘與體系中高分子鏈的數(shù)密度成正比��,因此����,所俘獲的亞穩(wěn)定納米有序結(jié)構(gòu)在實(shí)驗(yàn)上一般都具有分鐘或者小時(shí)量級(jí)的存在時(shí)間���,可以采用快速降溫至玻璃化轉(zhuǎn)變溫度以下或者使高分子鏈之間快速交聯(lián)等方法來進(jìn)行穩(wěn)定����。
我們分別采用組分的快速化學(xué)轉(zhuǎn)變、階躍剪切形變�����、快速壓力變化給出了構(gòu)造嵌段共聚物體系中不穩(wěn)定狀態(tài)的三種途徑���,系統(tǒng)研究了從這些不穩(wěn)定狀態(tài)出發(fā)的非平衡態(tài)結(jié)構(gòu)演化動(dòng)力學(xué)過程��,建立了與平衡態(tài)相圖完全不同的�����、由非平衡態(tài)結(jié)構(gòu)演化動(dòng)力學(xué)過程俘獲的結(jié)構(gòu)狀態(tài)的分布圖��。其中�,采用組分的快速化學(xué)轉(zhuǎn)變和快速壓力變化俘獲的納米有序結(jié)構(gòu)都是亞穩(wěn)定的�����,而采用階躍剪切形變俘獲的則都是假亞穩(wěn)定的納米有序結(jié)構(gòu)(橢球和橢圓柱等)�,即:擁有亞穩(wěn)定狀態(tài)的生存時(shí)間、但存在微弱殘余應(yīng)力的結(jié)構(gòu)�����。
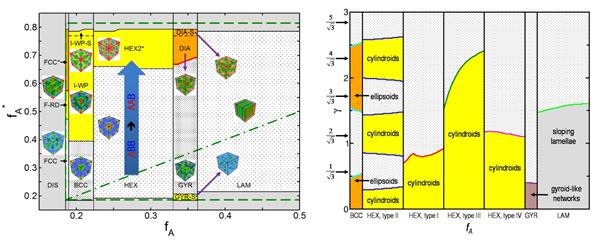
圖:由非平衡態(tài)結(jié)構(gòu)演化動(dòng)力學(xué)過程俘獲的結(jié)構(gòu)狀態(tài)的分布圖,分別采用組分的快速化學(xué)轉(zhuǎn)變(左圖)和階躍剪切形變(右圖)獲得��,其中���,左圖中的fA和fA*分別表示組分的快速化學(xué)轉(zhuǎn)變前后的A組分的體積分?jǐn)?shù)���,右圖中的γ表示階躍剪切應(yīng)變的大小�����。
2. 聚合物非平衡態(tài)場(chǎng)論研究及其數(shù)值運(yùn)算
基于柔性高斯鏈模型的聚合物自洽場(chǎng)理論是描述高分子復(fù)雜體系最為精確的平均場(chǎng)理論之一�����,在研究和預(yù)測(cè)高分子復(fù)雜體系的平衡態(tài)性質(zhì)方面取得了十分巨大的成功��。然而��,由于在獲取自洽場(chǎng)方程組時(shí)對(duì)組分空間密度分布和與組分空間密度分布相對(duì)應(yīng)的勢(shì)場(chǎng)都進(jìn)行了平均場(chǎng)近似(正解聚合物自洽場(chǎng)理論)���,目前的聚合物自洽場(chǎng)理論僅僅能夠獲取熱力學(xué)平衡狀態(tài)和亞穩(wěn)定狀態(tài)的性質(zhì)���,即自由能曲面上的全局最小值點(diǎn)和局域極小值點(diǎn)��,不能夠獲取不穩(wěn)定狀態(tài)的非平衡態(tài)性質(zhì)���。
為了能夠獲取高分子復(fù)雜體系中不穩(wěn)定狀態(tài)的非平衡態(tài)性質(zhì),我們建立了兩種反解聚合物自洽場(chǎng)理論的高效率新數(shù)值求解技術(shù)��。不同于正解聚合物自洽場(chǎng)理論時(shí)被研究體系的組分空間密度分布和與組分空間密度分布相對(duì)應(yīng)的勢(shì)場(chǎng)可以通過自洽迭代的方式同時(shí)進(jìn)行獲取�����,反解聚合物自洽場(chǎng)理論首先固定被研究體系的非平衡態(tài)組分空間密度分布����,然后再采用新建立的兩種迭代方法獲取與組分空間密度分布相對(duì)應(yīng)的勢(shì)場(chǎng)。因此,在被研究體系的組分空間密度分布已知的情況下,采用這兩種反解聚合物自洽場(chǎng)理論的高效率新數(shù)值求解技術(shù)可以獲取相應(yīng)自由能曲面上任意狀態(tài)的性質(zhì)�����,尤其是多種不穩(wěn)定狀態(tài)的非平衡態(tài)性質(zhì)(體系的自由能和組分的化學(xué)勢(shì)等),突破了傳統(tǒng)聚合物自洽場(chǎng)理論僅僅能夠研究熱力學(xué)平衡狀態(tài)和亞穩(wěn)定狀態(tài)的局限和計(jì)算技術(shù)瓶頸���。